Круглые тела - цилиндр, конус, шар, эллипсоид их виды и формулы (Таблица)
Круглые и некоторые другие тела (V — объем тела, S6 и S— его боковая и полная поверхности)
|
Круглые тела |
Обозначения |
Формулы |
|
Цилиндр
|
F и Р — площадь и периметр основания; h — высота; l — образующая; Q и s — площадь и периметр сечения, перпендикулярного к образующей. |
V = Fh = Ql; S6 = sl = Ph; S = sl + 2F = Ph + 2F. |
|
Прямой цилиндр
|
F и Р — площадь и периметр основания; l — образующая. |
V = Fl; S6 = Pl; S = Pl + 2F. |
|
Прямой круговой цилиндр
|
R — радиус основания; h — высота. |
V = πR2h; S6 = 2πRh; S = 2πR*(h + R). |
|
Цилиндр, усеченный непараллельно основанию
|
h1 и h2 — наименьшая и наибольшая образующие; l — длина отрезка, соединяющего центры тяжести оснований О и O1; Q и L — площадь и периметр сечения, перпендикулярного отрезку OOi. |
 |
|
Прямой круговой цилиндр, усеченный непараллельно основанию
|
R — радиус основания; h1 и h2 — наименьшая и наибольшая образующие. |
 |
|
Полный цилиндр (цилиндрическая труба)
|
R — наружный радиус; r — внутренний радиус; ρ = (R + r)/2 — средний радиус; h — высота; δ = R - r — толщина. |
 |
|
Конус
|
F — площадь основания; h — высота. |
V = 1/3*Fh |
|
Прямой круговой конус
|
R — радиус основания; h— высота; l = √(R2 + h2) — образующая. |
 |
|
Усеченный прямой круговой конус
|
R и r — радиусы оснований; h — высота; l — образующая: l = √(h2 + (R - r)2); H — высота неусеченного конуса: H = h + hr / (R - r). |
 |
|
Эллиптический конус (прямой) |
а, b — полуоси основания, h — высота |
 |
|
Усеченный эллиптический конус |
Параллельные основания — эллипсы с полуосями a, b и a1, Ь1; h — высота. |
 |
|
Полый шар
|
R — наружный радиус; r — внутренний радиус; D — наружный диаметр; d — внутренний диаметр. |
 |
|
Шаровой сегмент
|
h — высота сегмента; R — радиус шара; а — радиус основания сегмента: a = √(h(2R - h)) |
 |
|
Шаровой слой
|
h — высота слоя; а и Ь — радиусы оснований (а > Ь); R — радиус шара. |
где V1 — объем вписанного в шаровой слой усеченного конуса, радиусы оснований которого а и Ь, высота Л и образующая l; |
|
Шаровой сектор
|
h — высота сегмента; а — радиус основания сегмента; R — радиус шара. |
 |
|
Гор (цилиндрическое кольцо)
|
r — радиус поперечного сечения; R — расстояние центра поперечного сечения от оси вращения; D = 2R; d = 2r. |
 |
|
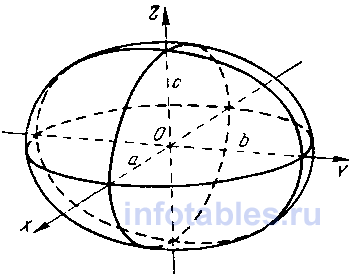
Эллипсоид
|
a, b, с — полуоси. | V = 4/3*πabc |
|
Эллипсоид вращения |
1) Ось вращения 2а (с = b). 2) Ось вращения 2Ь (с = а). |
 |
|
Сегмент эллиптического параболоида
|
a, b — полуоси эллипса (основания); h — высота. |
V = ½πabh. |
|
Сегмент параболоида вращения
|
r — радиус основания; h — высота. |
V = ½πr2h |
|
Усеченный параболоид вращения
|
R и r — радиусы параллельных оснований; h — высота. |
V = ½πh*(R2 + r2) |